Light || Definition, Nature, Reflection & Properties
Light Light enables us to see things around us. This is a form of energy that we can detect with…
Table of Contents
Light
- Light enables us to see things around us.
- This is a form of energy that we can detect with our eyes.
- It falls on objects, bounces off from their surfaces and reaches our eyes.
- It is the light that causes the sensation of vision in us.

- For example, the sun gives out light, therefore we can see the sun.
- It takes about 8.3 minutes to reach the earth from the sun.
- Thomas Alva Edison was the first person who invented electric light bulb.
Definition of Light
- Light is a form of energy which enables us to see objects which emit or reflect light.
- We get it from various sources, e.g. sun, electric lamp, candle, and oil lamp, etc.
Characteristics of Light
- It is an electromagnetic wave.
- It is a transverse wave, and does not need any medium to travel.
- They can travel through vacuum.
- Its speed through vacuum is 3 x 108 m/s.
- There velocity changes when it travels from one medium to another. While frequency remain same in all medium.
- It can pass through transparent materials, such as glass or air.
- They travel in a straight line.
- It gets reflected back from polished surfaces, such as mirrors, polished metal surfaces, etc.
- It undergoes refraction when it travels from one transparent medium to another.
Rectilinear Propagation of Light
- There are a number of everyday phenomena which suggest that light travels in straight lines:-
- Formation of day and night suggests.
- Formation of shadows suggests.
- When a beam of sunlight enters a dark room through a ventilator, we can see the light.
- When the head light of a car is switched on, there rays appear to travel in straight lines.
- The burning candle flame, it appears as if it is giving out a few beams of light.
- Beams of light coming from the projection room in the cinema hall.
- The ray coming from small laser torches used as pointers.
- Above all the given examples are suggest that light travels in a straight line.
- Rectilinear propagation of light refers to the property of light travelling in a straight line.
- Also read on touching the link:-
About related to machine click on the link
Nature of Light
- There are two theories about the nature of light:-
1. Wave theory
2. Particle theory
1. Wave theory
- According to wave theory, light consists of electromagnetic waves which do not require a material medium for their propagation.
- The wavelength of visible light waves is very small i.e only about ( 4× 10-7 to 8 × 10-7 )m.
- The speed of light wave is very high.
- And it tells about the phenomena of diffraction ( bending of light around the corners of tiny objects), interference and polarization of light.
2. Particle theory
- According to the particle theory, light is composed of particles which travel in a straight line at very high speed.
- It tells about the phenomena of reflection and refraction of light, and casting of shadows of objects.
Conclusion
- In the past hundred years of physics experiment have demonstrated that light has a dual nature, it exhibits the properties of both waves and particles.
- The modern theory of light called “Quantum Theory of Light”. It combines both the wave and particle models of light.
Ray and Beam of Light
- A straight line drawn in the direction of propagation of light is known a ray of light.
- A ray is described by a straight line with an arrow- head pointing in the direction of propagation of light.
- A bundle of the adjacent light rays is called a beam of light.
- A beam of light can be
- Parallel beam
- Convergent beam
- Divergent beam of light.
- The beam of light in which all the rays are parallel to each other is called parallel beam of light.
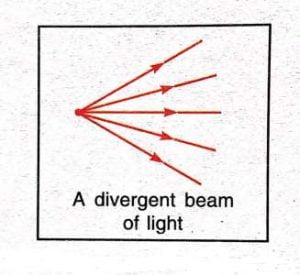
- The beam of light in which the rays of light starting from a point source move out in different directions is called a divergent beam of light.
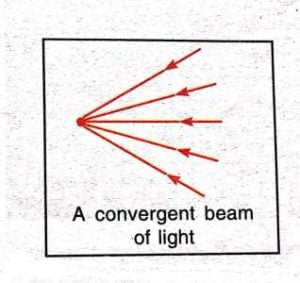
- The beam of light in which the rays of light starting from a large source of light get closer to each other is called convergent ray of light.
Reflection of Light
- When a ray of light falls on a polished smooth surface, such as a mirror, it return back into the same medium.
- Hence, the bouncing back of light after striking the surface of an object is called reflection of light.
- Different materials reflect light to different extent.
- Silver is one of the best reflectors of light.
- We see our images in a mirror due to reflection of light.
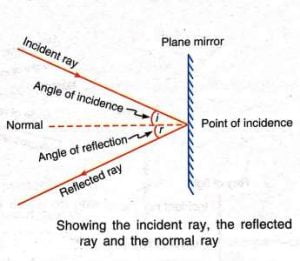
- The ray of light which falls on a cleaned surface is called the incident ray of light.
- The ray of light which gets reflected from a polished surface is called the reflected ray of light.
- The normal is a line at right angle to the reflecting surface, such as, a plane mirror, at the point of incidence.
- The angle made by the incident ray with the normal is known the angle of incidence( <i ).
- The angle made by the reflected ray with the normal is called the angle of reflection( <r ).
Kinds of reflection
- Depending on the nature of the reflecting surface, there could be two kinds of reflections:-
1. Regular reflection
2. Irregular reflection
1. Regular reflection
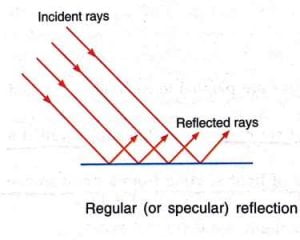
- The reflection of light from a mirror- like smooth reflecting surface so that the reflected rays are parallel to each other is called regular reflection.
- It is also known as specular reflection.
2. Irregular reflection
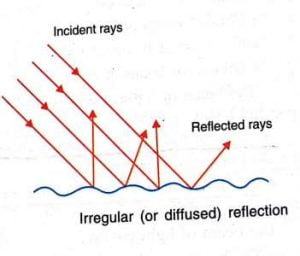
- The reflection of light from a rough, irregular surface randomly in various directions is called irregular reflection.
- It is not parallel to each other.
- It is also called diffused reflection.
Laws of Reflection of Light
- The reflection of light from a plane surface or from a spherical surface takes place according to the two laws, which are known as the laws of reflection.
1. First law of reflection
2. Second law of reflection
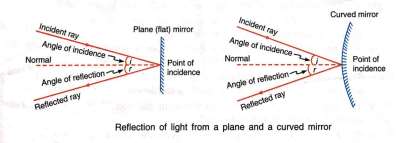
1. First law of reflection
- The angle made by the incident ray with the normal at the point is equal to the angle made by the reflected ray with the normal, i.e.
Angle of incidence = Angle of reflection
<i = <r
2. Second law of reflection
- The incident ray, the reflected ray and the normal at the point of incidence, all lie in the same plane.
Images formed by reflection
- The images formed by the reflection, it may be real or virtual.
1. Real image
- When the rays of light starting from a well illuminated object are reflected from a smooth polished surface in such a way that they meet at some other point or on a screen, then image so formed is called real image.
- A concave mirror gives a real image if the object is placed at or beyond focus.
Following are the characteristics of a real image:-
- It can always be taken on screen.
- It is always inverted as compared to the object.
- It may be of the same size/bigger/smaller than the object.
2. Virtual image
- When the rays of light starting from a well illuminated object are reflected from a smooth polished surface in such a way that they appear to meet at some other point, but cannot meet on a screen, then the image so formed is called virtual image.
- The image formed in a looking glass is always virtual.
Following are the characteristics of a virtual image:-
- It cannot be taken on a screen.
- It is always erect as compared to the object.
- It may be of the same size/bigger/smaller than the object.
Refraction of Light

- We know that light travels in straight line through any medium of uniform density.
- However, when a ray of light travels from one transparent medium to another, it suffers a change in its direction.
- For e.g, air to glass, etc.
- The change in direction of a ray of light when it passes from one medium to another, is called refraction of light.
- Its speed through glass is 2 x 108 m/s.
or
- The bending of a ray of light when it passes from one medium to another, is called refraction of light.
- The direction in which the ray of light bends when it travels from one medium to another depends upon the optical density of the two media.
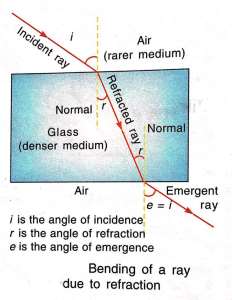
- When a ray of light goes from an optically rarer medium to an optically denser medium, it bends towards the normal. i.e.
Angle of refraction( <r ) < Angle of incidence ( <i )
- When a ray of light goes from an optically denser medium to an optically rarer medium, it bends away from the normal. i.e.
Angle of refraction ( <r ) > Angle of incidence (<i )
- Air is optically less denser than water or glass. Therefore
- A ray of light travelling from air into glass bends towards the normal.
- A ray of light travelling from glass into air bends away from the normal.
Laws of Refraction of Light
- There are two laws of refraction:-
1. First law of refraction
2. Second law of refraction
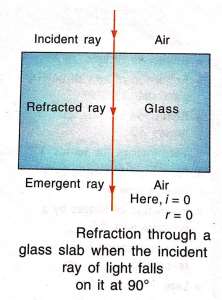
1. First law of refraction
- It tells about the ratio of sine of the angle of incidence to the sine of the angle of refraction for a particular pair of media is constant.
- Hence, if the angle of incidence is i, and that of refraction is r, then
sine of the angle of incidence/ sine of the angle of refraction = sin i/ sin r = constant
- The value of this constant depends upon temperature and the wavelength of light used in the measurement.
- It is also known as Snell’s law.
2. Second law of refraction
- It tells that the ray, the refracted ray and the normal at the point of incidence, all lie in the same plane.
Cause of Refraction of light
- The speed of light depends on the nature of the medium in which it travels.
- When it travels from a rarer medium to a denser medium, its speed decreases.
- Whereas speed of light increases when it travels from a denser to a rarer medium.
- It is due to this change in the speed of light that the ray of light bends as it goes from one medium to another.
- Thus, the change of speed of light as it travels from one medium to another is the cause of refraction.
Effects of Refraction of Light
- A stick held obliquely and partly immersed in water, it appears to be bent at the water surface.
- An object submerged under water appears to be raised.
- A pool of water is appeared to be less deep than it actually is.
- When a thick glass slab is placed over some printed matter, the letters seem raised when viewed from the top.
- A lemon is kept in water in a glass tumbler appears to be bigger than its actual size, when viewed from the sides.
- The stars appear to sparkle on a clear night.
Let’s known more
1. Define luminous objects.
Ans:- The objects which emit light themselves are called luminous objects.
- Luminous objects may be natural or man-made.
2. Define non-luminous objects.
Ans:- Those objects which do not emit light themselves but only reflect ( or scatter ) the light which falls on them, are called non-luminous objects.
- Even the moon is a non-luminous objects. We can see the moon because it reflects the sunlight falling on its surface towards us.
3. What is transparent medium?
Ans:- A medium in which ray can travel freely over large distances is called a transparent medium. For e.g. water, glycerine etc.
4. What is opaque?
Ans:- A medium in which ray cannot travel is called opaque. For e.g. wood, metals, bricks, etc.
5. Define medium.
Ans:- The material through which ray travels is called medium.
Comments